Question

17. The table below shows the population of Mexico from 2010 to 2019.YearPopulation (millions)2010114.12011115.72012117.32013118.82014120.42015121.92016123.32017124.82018126.22019127.6(a) Use a graphing calculator or spreadsheet program to build an exponential regression model to fit this data, letting t=0 in 2010, where Pt is measured in millions of people. Round each coefficient to two decimal places.Pt = (b) What does this model predict that the population of Mexico will be in 2040? Round your answer to the nearest tenth (a hundred thousand people). million people(c) When does this model predict that Mexico's population will reach 145 million? Give your answer as a calendar year (ex: 2010).During the year

Answer 1

The exponential regression model that fits the data is;

`P_t=114.38(1.01^t)`

(b) In 2040;

`t=40`

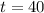
Thus, the model predicts that the population of mexico will be;

`\begin{gathered} P_(40)=114.38(1.01^(40)) \\ P_(40)=170.3 \end{gathered}`

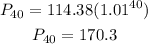
The model predicts that the population of mexico will be 170.3 million people.

(c) When the population of mexico reach 145 million, the year will be;

`\begin{gathered} 145=114.38(1.01^t) \\ 1.01^t=(145)/(114.38) \\ \\ \end{gathered}`

So, we have;

`\begin{gathered} 1.01^t=1.2677 \\ t=23.84 \\ t\approx24 \end{gathered}`

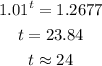
During the year 2024.