Question

Mei invests $3,147 in a retirement account with a fixed annual interest rate compounded 12 times per year. After 13 years, the balance reaches $6,754.96. What is the interest rate of the account?

Answer 1

Step-by-step explanation:

Using the compound interest formula:

`FV\text{ = P(1 +}(r)/(n))^(nt)`

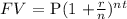
where Fv = future value = $6,754.96

P = principal = $3,147

r = rate = ?

n = number of times compounded = 12 times

t = time = 13 years

Inserting the values into the formula:

`6754.96\text{ = 3147(1 + }(r)/(12))^(12*13)`
`\begin{gathered} 6754.96\text{ = 3147(1 + }(r)/(12))^(156) \\ \\ \text{divide both sides by 3147:} \\ \frac{6754.96\text{ }}{3147}\text{= }\frac{\text{3147}}{3147}\text{(1 + }(r)/(12))^(156) \\ 2.1465\text{ = (1 + }(r)/(12))^(156) \\ \end{gathered}`
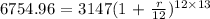
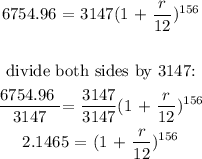
`\begin{gathered} we\text{ take the 156th root of both sides} \\ \sqrt[156\text{ }]{2.1465}\text{ = }\sqrt[156\text{ }]{\text{ (1 + }(r)/(12))^(156)} \\ 1.0049\text{ = (1 + }(r)/(12)) \\ \end{gathered}`
`\begin{gathered} \text{subtract 1 from both sides:} \\ 1.0049\text{ - 1 = 1- 1 + }(r)/(12) \\ 0.0049\text{ = 0 + r/12} \\ 0.0049\text{ = }(r)/(12) \\ mu\text{ltiply both sides by 12:} \\ 0.0049(12)\text{ = 12(r/12)} \\ r\text{ = }0.0588 \\ \text{rate = 5.88\%} \end{gathered}`

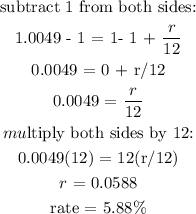
The interest rate of the account is 5.88%