Question

Solve the triangle. B=36 a=41 c=20

Answer 1

use cosine rule:-
b^2 = 41^2 + 20^2 - 2*20*41*cos 36

= 754.21

b = 27.5

you can now find angle A using the sine rule

27.5 / sin 36 = 41 / sin A

sin A = 0.87633

< A = 61.2 degrees

Answer 2

b= 27.46

A= 61 degree

C= 83 degree

Explanation:

Solve the triangle. B=36 a=41 c=20

Apply cosine rule to find the side length B

`b^2= a^2 +c^2-2acsin(A)`

`b^2 = 41^2 + 20^2 - 2 \cdot 20 \cdot 41 \cdot cos 36`

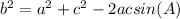
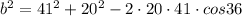
Take square root on both sides

so b=27.46292

b= 27.46

Now use sine rule to find the angles A and C

`(Sin A)/(a) = (Sin B)/(b)`

`(Sin A)/(41) = (Sin 36)/(27.46)`

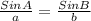
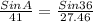
Cross multiply it

`27.46 sin(A)= 41 sin(36)`

`Sin(A) = (41 Sin 36)/(27.46)`

A=
`sin^(-1)((41 Sin 36)/(27.46))`

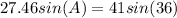
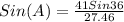
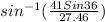
A= 61 degree

Angle A + angle B + angle C= 180

`61+36 + angle C= 180`

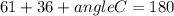
Angle C= 83 degree