The diagram of the square is shown in the first picture below
We have the radius
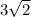
and the triangle formed is an isosceles triangle
We can start by finding out the length of one side of the square. A square has four sides of equal length and the length of the diagonal is twice the length of the radius. So, by using the Pythagoras theorem we have
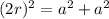
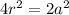
, substitute
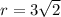
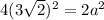
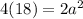
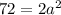
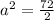
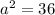
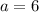
Then we'll use Pythagoras theorem again to find the length of the Apothem
We need to halve the length of one side of the square to obtain the other short side of the right angle triangle, so 6÷2 =3
apothem² = (3√2)² + 3²
apothem² = 18+9
apothem² = 27
apothem = √27 = 3√3