Question

Which matrix represents the solution to the system of equations below?2a+b+c=2-a+b-c=-4a-2b+2c=6O00 201 0-200 1 01 00 10-200 1 0Previous ActivityNext Activit

Answer 1

Step-by-step explanation:

The equations are given below as

`\begin{gathered} 2a+b+c=2 \\ -a+b-c=-4 \\ a-2b+2c=6 \end{gathered}`

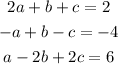
isolate a in equation (1) to give

`a=(2-b-c)/(2)`

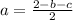
Susbtitute the equation of a in equation (2) and (3)

`\begin{bmatrix}-(2-b-c)/(2)+b-c=-4\\ (2-b-c)/(2)-2b+2c=6\end{bmatrix}`

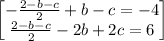
Simplifying the equation, we will have

`\begin{bmatrix}(3b-c-2)/(2)=-4\\ (-5b+3c+2)/(2)=6\end{bmatrix}`

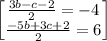
Isolate b from the equation below

`\begin{gathered} \begin{equation*} (3b-c-2)/(2)=-4 \end{equation*} \\ b=(c-6)/(3) \end{gathered}`

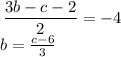
substiuting , we will have

`\begin{bmatrix}(-5\cdot (c-6)/(3)+3c+2)/(2)=6\end{bmatrix}`

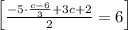
On simplifying , we will have

`\begin{gathered} \begin{bmatrix}(2\left(c+9\right))/(3)=6\end{bmatrix} \\ 2c+18=18 \\ 2c=18-18 \\ 2c=0 \\ c=0 \end{gathered}`
`\begin{gathered} b=(c-6)/(3) \\ b=(0-6)/(3) \\ b=-(6)/(3) \\ b=-2 \end{gathered}`
`\begin{gathered} a=(2-b-c)/(2) \\ a=(2-(-2)-0)/(2) \\ a=(2+2)/(2) \\ a=(4)/(2) \\ a=2 \end{gathered}`

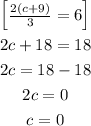
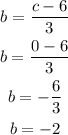
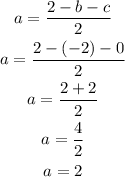
Hence,

The final answers are

`a=2,b=-2,c=0`

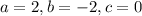
The final answer is