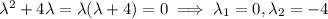Question

(1 point) suppose that the trace of a 2×22×2 matrix aa is tr(a)=−4tr(a)=−4, and the determinant is det(a)=0det(a)=0. find the eigenvalues of aa.

Answer 1

Suppose


`\mathbf A=\begin{bmatrix}a&b\\c&d\end{cases}`

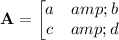
with
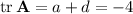
`\mathrm{tr}\,\mathbf A=a+d=-4` and
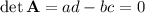
`\det\mathbf A=ad-bc=0`. We can find the eigenvalues of
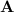
`\mathbf A` in the usual way, by taking the determinant of
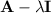
`\mathbf A-\lambda\mathbf I` and setting it equal to 0.


`\begin{vmatrix}a-\lambda&b\\c&d-\lambda\end{vmatrix}=(a-\lambda)(d-\lambda)-bc=\lambda^2-(a+d)\lambda+(ad-bc)`

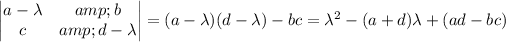
and we observe that the characteristic polynomial has linear coefficient
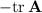
`-\mathrm{tr}\,\mathbf A` and constant coefficient
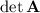
`\det\mathbf A`. Thus in this case we have the characteristic polynomial equation,


`\lambda^2+4\lambda=\lambda(\lambda+4)=0\implies\lambda_1=0,\lambda_2=-4`