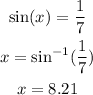Question

The inverse trig ratios should be thought of as undoing and operation much the same way we consider multiplication and division as inverses, or addition and subtraction. So long as we are dealing with acute angles in a right triangle, we can use inverse trig ratios to solve equations involving trig ratios. Solve the following example for x (in degrees), by taking the inverse sine of both sides. Round your answer to two decimal plaſes. sin(x)=1/7

Answer 1

We have to solve the equation:

`\sin (x)=(1)/(7)`

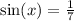
To solve for an angle of a trig ratio, we take the inverse trig of the "constant" to the other side. That will let us solve for the "angle".

Thus, we can take the inverse sine of 1/7th to get the value of the angle "x".

Shown below:

`\begin{gathered} \sin (x)=(1)/(7) \\ x=\sin ^(-1)((1)/(7)) \\ x=8.21\degree \end{gathered}`