Question

The function F(x) = 6x-2/5 is an example of a rational function.
A. True
B. False

Answer 1

By definition, a rational function, is an algebraic expression that includes a term in fractional form containing polynomials. To illustrate more clearly, this is an example of a rational function:


`f(x)= ( 3x^(2)+2 )/(5 x^(3)+2x )`

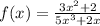
Basically, a rational function must have polynomials in both the numerator and denominator of the fractional term. Since the given function f(x)= 6x-2/5 only contains a polynomial on the numerator, this is not a rational function. The denominator is a constant, not a polynomial.

The answer is false.

Answer 2

The statement about "The function F(x) = 6x-2/5 is an example of a rational function." is false. The answer is letter B. The definition of a rational polynomial is that it is written in a form in which a polynomial is divided by a polynomial. Yes, 6x - 2 is a polynomial, a binomial to be precise but the 5 itself is not. It is not a polynomial, let alone a monomial because it does not contain a variable x or y. It is only a number. And so the statement is false.