Question

Identify the compositions performed on ΔXYZ to map onto ΔX″Y″Z″.a. Reflection along the line y = x; 180° rotation about the originb. Translation: (x,y) → (x – 2,y + 1); 180° rotation about the originc. Reflection along y-axis; 180° rotation about the origind. Translation: (x,y) → (x + 2,y – 1); 180° rotation about the origin

Answer 1

The coordinates of X,Y,Z are given below as

`\begin{gathered} X(x,y)\Rightarrow(5,2) \\ Y(x,y)\Rightarrow(2,-1) \\ Z(x,y)\Rightarrow(7,-3) \end{gathered}`

The coordinates of X',Y',Z' are given below as

`\begin{gathered} X^(\prime)(x,y)\Rightarrow(3,3) \\ Y(x,y)\Rightarrow(0,0) \\ Z^(\prime)(x,y)\Rightarrow(5,-2) \end{gathered}`

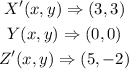
To figure out the translation between this two points, we will have

`\begin{gathered} (5-3),(2-3)\Rightarrow(2,-1) \\ \text{Hence, the translation will be} \\ (x,y)\Rightarrow(x-2),y+1) \end{gathered}`

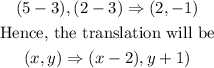
The coordinates of X'',Y'',Z'' are given below as

`\begin{gathered} X^(\doubleprime)(x,y)\Rightarrow(-3,-3) \\ Y^(\doubleprime)(x,y)\Rightarrow(0,0)_{} \\ Z^(\doubleprime)(x,y)\Rightarrow(-5,2) \end{gathered}`

180 Degree Rotation

When rotating a point 180 degrees counterclockwise about the origin our point A(x,y) becomes A'(-x,-y). So all we do is make both x and y negative.

Hence,

The final answer is

B) Translation: (x,y) → (x – 2,y + 1); 180° rotation about the origin