Question

Greg is trying to solve a puzzle where he has to figure out two numbers, x and y. Three less than two-third of x is greater than or equal to y. Also, the sum of y and two-third of x is less than 4. Which graph represents the possible solutions?

Answer 1

in other words b

Explanation:

Answer 2

inequation 1:


`(2)/(3)x-3 \geq y`

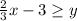
to plot the pairs (x, y) for which the inequation holds, draw the line
`y=(2)/(3)x-3`

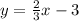
then pick a point in either side of the line. If that point is a solution of the inequation, than color that region of the line, if that point is not a solution, then color the other part of the line.

we do the same for the second inequation. Then the solution, is the region of the x-y axes colored in both cases.

inequation 2:


`y+ (2)/(3)x\ \textless \ 4`


`y\ \textless \ - (2)/(3) x+ 4`


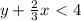
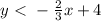
draw the lines

i)
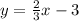
`y=(2)/(3)x-3` use points (0, -3), (3, -1)

ii)
`y=- (2)/(3) x+ 4` use points ( 0, 4), (3, 2)


let's use the point P(3, 3) to see what region of the lines need to be coloured:


`(2)/(3)x-3 \geq y` ;

`(2)/(3)(3)-3 \geq 3`

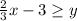
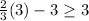
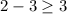
`2-3 \geq 3`, not true so we color the region not containing this point



`y+ (2)/(3)x\ \textless \ 4`

`(3)+ (2)/(3)(3)\ \textless \ 4`

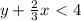
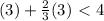
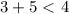
`3+ 5\ \textless \ 4` not true, so we color the region not containing the point (3, 3)

The graph representing the system of inequalities is the region colored both red and blue, with the blue line not dashed, and the red line dashed.