Question

A car leaves a town at 40 kilometers per hour. How long will it take a second car, travelling at 85 kilometers per hour, to catch the first car if

it leaves 1 hour later?
Amount of Time (in hours): |

Answer 1

The second car will catch up to the first car after 8/9th of an hour

SOLUTION

Problem Statement

The question tells us a car leaves a town with a speed of 40km/hr and we are required to find how long it will take a second car that begun the same journey an hour after, moving at 85km/hr to catch the first car.

Method

To solve this question, we only require two things:

1. Sound logical reasoning.

2. Formula for Distance calculation.

The formula is:

`\text{Distance}=\text{Speed}*\text{time}`

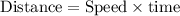
Solution

Before we proceed to solve, we need to understand the question very well. The question says that car 2 catches up with car 1 after some time. This also implies that both car 1 and car 2 would have traveled the exact same distance when car 2 catches up with car 1.

This, therefore, means that if we can find the expression for the distance traveled by both cars, we can equate them.

This leads us to our first step for the solution.

Step 1: Working with the distance

Let us assume that the first car has moved a total of X kilometers after time t1, when the second car catches up to it.

This means that the distance covered by the first car can be written using the formula given above:

`\begin{gathered} \text{ Distance}=Speed* time \\ \text{Distance moved by car 1 = X} \\ \text{speed of car 1 = 40} \\ \text{time taken for car 1 to move through distance X= }t_1 \\ \\ \therefore X=40t_1 \end{gathered}`

Similarly, we can find an expression for the distance moved by the second car as follows:

`\begin{gathered} \text{Distance moved by car 2 = X} \\ \text{speed of car 2 = 85} \\ \text{time taken for car 2 to move through distance X = }t_2 \\ \\ \therefore X=85t_2 \end{gathered}`

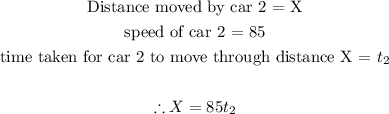
Since the two expressions are the expressions for the same distance covered by both cars after times t1 and t2 respectively, then we can equate them together and find an expression relating t1 to t2. This is shown below:

`\begin{gathered} X=40t_1=85t_2 \\ (40t_1)/(5)=(85t_2)/(5) \\ \\ \therefore8t_1=17t_2\text{ (Equation 1)} \end{gathered}`

Step 2: Working with the time

Also, we are told that the second car takes off 1 hour after the first car. We can also deduce that the time taken for car 2 to meet up with car 1, is 1 hour less. This means that t2 is less than t1 by 1 hour.

Thus, we can write:

`t_1=t_2+1\text{ (Equation 2)}`

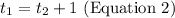
Step 3: Solving both equations simultaneously

Now that we have the two equations in terms t1 and t2, we can proceed to solve them simultaneously.

We shall take Equation 2 and substitute it into Equation 1.

`\begin{gathered} t_1=t_2+1 \\ \text{taking this expression for }t_1\text{ and substitute it into Equation 1} \\ 8(t_2+1)=17t_2 \\ \text{Expand the bracket, we have:} \\ 8t_2+8=17t_2 \\ \text{subtract }8t_2\text{ from both sides} \\ 8=17t_2-8t_2 \\ 8=9t_2 \\ \text{Divide both sides by 9} \\ (8)/(9)=t_2 \\ \\ \therefore t_2=(8)/(9)hr \\ t_2=(8)/(9)*60=53.\bar{3}\text{ minutes} \end{gathered}`

Final answer

Thus, the second car will catch up to the first car after 8/9th of an hour