Question

Let V=R2 and let H be the subset of V of all points on the line 4x−3y=−12. Is H a subspace of the vector space V?1. Is H closed under addition? If it is, enter CLOSED. If it is not, enter two vectors in H whose sum is not in H, using a comma separated list and syntax such as <1,2>, <3,4>.2. Is H closed under scalar multiplication? If it is, enter CLOSED. If it is not, enter a scalar in R and a vector in H whose product is not in H, using a comma separated list and syntax such as 2, <3,4>

Answer 1

H does not contain the zero vector.

Not closed under addition. Example <-3, 0>, <4, 0>

Not closed under scalar multipication. Example 2, <-3, 0>

Step-by-step explanation:

The zero vector, in this case, is the point (0,0). Now the question is whether (0,0) lies on the line.

To find out, let us put x -0 and y= 0 into our equation and see if it is satisfied.

`4(0)-3(0)=-12`
`\Rightarrow0=-12`

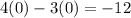
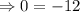
which is not true, Hence (0.0) is not contained in H.

Let us not test for closure under addition.

Imagine taking two vectors that lie along the line as shown below.

Then their sum

does not lie on the line (the green arrow does not end at the red line). Therefore, H is not closed under addition.

One example is additing vectors ( points) (0, -3) and (4, 0). Their sum is ( 0 + 4, -3 + ) = ( 4, -3) which does not lie on the red line.

Let us now look at scalar multipication.

Scaling the above vector ( the blue line) just lengthens it.

which is a vector that does not lie on the red line. This tells us that H is not closed under scalar multiplication.

An example would be scalar 2 and the vector ( - 3, 0). The multiplication 2(-3,0) = (-6, 0_ gives a vector (-6, 0) that does not lie on the line.

Since H does not satisfy any of the three conditions for being a subspace, it is not a subspace of R^2.