Question

I got the range correct but can’t find the answer for s=____psi

Answer 1

426.6

Step-by-step explanation

We want to find the Standard deviation of the data given.

To do this, we will use the formula:

`\begin{gathered} SD=\sqrt{\frac{\sum (x\text{ - }\mu)^2}{n}} \\ \text{where }\mu\text{ = mean of the data} \end{gathered}`

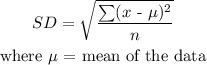
Let us first find the mean:

`\begin{gathered} \mu\text{ = }\frac{3990\text{ + 412}0\text{ + 3500 + 3100 + }2990\text{ + 3810 + 4120 + 4020 }}{8} \\ \mu\text{ = }(29560)/(8) \\ \mu\text{ = 3695} \end{gathered}`

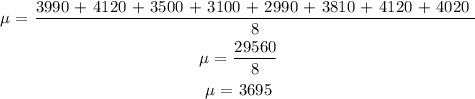
Now, we will subtract the mean from each number in the set of data(x - u):

3990 - 3695 = 295

4120 - 3695 = 425

3500 - 3695 = -195

3100 - 3695 = -595

2990 - 3695 = -705

3810 - 3695 = 115

4120 - 3695 = 425

4020 - 3695 = 325

Now, square each of those values and add them:

`\begin{gathered} \sum (x\text{ - }\mu)^2=(295)^2+(425)^2+(-195)^2+(-595)^2+(-705)^2+(115)^2+(425)^2+(325)^2 \\ \sum (x\text{ - }\mu)^2\text{ = 87025 + 180625 + 38025 + 354025 + 497025 + 13225 + 180625 + 105625} \\ \sum (x\text{ - }\mu)^2\text{ = }1456200 \end{gathered}`

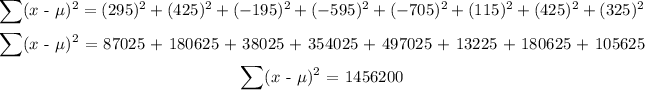
Now, divide by the number of data points (8):

`\begin{gathered} \frac{\sum (x\text{ - }\mu)^2}{n}\text{ = }(1456200)/(8) \\ \frac{\sum (x\text{ - }\mu)^2}{n}\text{ = }182025 \end{gathered}`

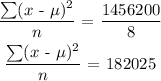
Now, find the square root:

`\begin{gathered} SD\text{ = }\sqrt{\frac{\sum (x\text{ - }\mu)^2}{n}}\text{ = }√(182025) \\ SD\text{ = 426.6} \end{gathered}`

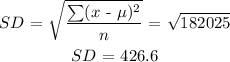
That is the answer.