Question

The depreciating value of a semi-truck can be modeled by y = Ao(0.83)x, where y is the remaining value of the semi, x is the time in years, and it depreciates at 17% per year.

An exponential function comes down from the positive infinity and passes through the points zero comma seventy thousand. The graph is approaching the x-axis. What is the value of the truck initially, Ao, and how would the graph change if the initial value was only $50,000?

$70,000, and the graph would have a y-intercept at 50,000
$60,000, and the graph would have a y-intercept at 70,000
$70,000, and the graph would fall at a slower rate to the right
$70,000, and the graph would fall at a faster rate to the right

Answer 1

Option A is correct.

Explanation:

We are given that, the model for the depreciating value of a semi-truck is,

`y = A_(O)(0.83)^x`

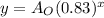
1. It is required to find the value of the truck initially i.e. when x= 0.

So, substituting x= 0, we have,

`y = A_(O)(0.83)^0`

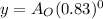
i.e.
`y = A_(O)* 1`

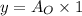
i.e.
`y = A_(O)`

Since, the graph passes through the point (0,70,000).

Thus, we get,
`A_(O)=70,000`

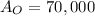
Hence, the initial value is 70,000.

2. It is required to find the value of the truck initially i.e. when x= 50,000

That is, when x= 0, the value of y= 50,000.

Graphically, it means that the graph would cut y-axis at the point (0,50,000).

Thus, the y-intercept would be at 50,000.

Change in the initial value will not have any affect on the rate of the graph.

So, from the above, we get,

Option A is correct.

Answer 2

The exponential graph is shown below.

The initial value when the time is zero is 70000. An initial value is normally shown as the point where the graph crosses the y-axis.

If the initial value was to be 50000, the curve would have crossed the y-axis at 50000

The correct answer is the first statement