Answer:
Part 1)

Part 2)
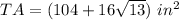
Explanation:
Part 1) Find the lateral area of the prism
we know that
The lateral area of the prism is equal to
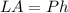
where
P is the perimeter of the base
h is the height of the prism
Applying the Pythagoras Theorem
Find the hypotenuse of the triangle
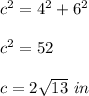
Find the perimeter of triangle
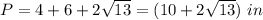
Find the lateral area
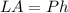
we have
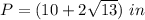
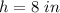
substitutes
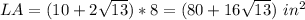
Part 2) Find the total area of the prism
we know that
The total area of the prism is equal to
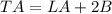
where
LA is the lateral area of the prism
B is the area of the base of the prism
Find the area of the base B
The area of the base is equal to the area of the triangle
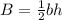
substitute
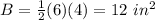
Find the total area of the prism
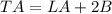
we have
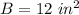

substitute
