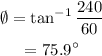The weight of the ladder is,
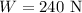
The coefficient of friction between the ladder and the floor is,
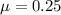
The diuagram of the forces is given below:
The force on point Q is equal to the weight of the ladder. we can write,

The force at point P will be equal to the frictional force. we can write,
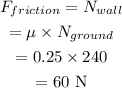
The resultant of these two forces is,
![\begin{gathered} F=\sqrt[]{240^2+60^2} \\ =247\text{ N} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/physics/high-school/cscyn0k5cfynpens72mn.png)
The angle with the horizontal is,