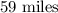ANSWER
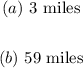
Step-by-step explanation
We are given an equation that represents the total length of the road:
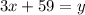
This equation is a linear equation. The general form of a linear equation is:

where m = slope/rate of change
b = y-intercept
(a) The change per day in the road's length is represented by the slope/rate of change of the equation.
Comparing the given equation with the general equation, we see that the rate of change is 3.
Therefore, the change per day in the road's length is:
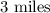
(b) The road's length when the crew started working represents the initial value of the length of the road. This is represented by the y-intercept of the equation.
Comparing the given equation with the general equation, we see that the y-intercept is 59.
Therefore, the road's length when the crew started working is: