Answer:
(D)

Explanation:
It is given from the figure that m∠BAC=48° and arcAC=110°.
The Inscribed Angle Theorem states that the measure of an inscribed angle is half the measure of its intercepted arc.
Now, using the above property, we have
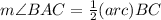
Substituting the given values, we get
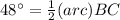

Thus, the measure of the arc BC is 96 degrees.
Hence, option D is correct.