Question

If x:y =a:b, prove that a:x=(a+b):(x:y)

Answer 1

We start by writing the ratio
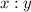
`x:y` and
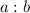
`a:b` as fraction


`(x)/(x+y): (y)/(x+y) = (a)/(a+b): (b)/(a+b)`

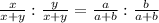
This shows two pairs of equivalent fractions


`(x)/(x+y)= (a)/(a+b)` and
`(y)/(x+y)= (b)/(a+b)`

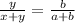
We will use the first pair of fraction

`(x)/(x+y)= (a)/(a+b)` ⇒ cross multiply gives

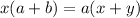
`x(a+b)=a(x+y)` ⇒ then rearrange

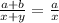
`(a+b)/(x+y) = (a)/(x)` ⇒ which we can also write in form of ratio

`(a+b):(x+y)=a:x`

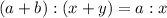
Hence it is proved that
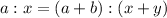
`a:x=(a+b):(x+y)` as required