Question

If sin θ = 1/3 and tan θ < 0, what is the value of cos θ?

Answer 1

`\bf sin(\theta)=\cfrac{opposite}{hypotenuse} \qquad cos(\theta)=\cfrac{adjacent}{hypotenuse} \quad % tangent tan(\theta)=\cfrac{opposite}{adjacent}\\\\ -------------------------------\\\\ sin(\theta )=\cfrac{1}{3}\cfrac{\leftarrow opposite}{\leftarrow hypotenuse}\impliedby \begin{array}{llll} \textit{so, let's use the pythagorean}\\ \textit{theorem to get the adjacent} \end{array}`


`\bf c^2=a^2+b^2\implies \pm√(c^2-b^2)=a\qquad \begin{cases} c=hypotenuse\\ a=adjacent\\ b=opposite\\ \end{cases} \\\\\\ \pm√(3^2-1^2)=a\implies \pm√(8)=a\implies \pm2√(2)=a`

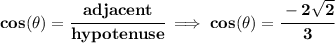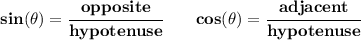
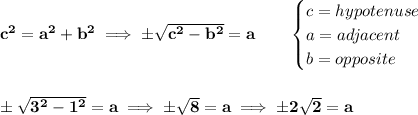
so hmmm which is it, the +/-? well, we know that tan(θ) < 0, that means the tangent of the angle is negative, well, the tangent is opposite/adjacent, the only way that fraction can be negative, is that if either, no both, just either opposite or adjacent is negative.

well, we know the opposite is +1, so, the adjacent then has to be negative, so is -2√(2) then


`\bf cos(\theta)=\cfrac{adjacent}{hypotenuse}\implies cos(\theta)=\cfrac{-2√(2)}{3}`