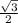Question

What is the cos 30°?

Answer 1

Its (sqrt(3))/2
Hope it helps.

Answer 2

cos 30 =
`(√(3) )/(2)`

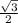
Explanation:

We know that in a right triangle, the length of an opposite side of 30 degrees is half of the length of hypotenuse.

Let "d" is the hypotenuse of the right triangle.

The opposite side = d ÷ 2

Using the Pythagorean theorem, we can find the third side.

`Thirdside^2 = d^2 - ((d)/(2)) ^(2)`

=
`d^2 - (d^2)/(4)`

=
`((4d^2 - d^2)/(4) )`

=
`(3d^2)/(4)`

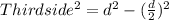
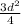
Taking square root on both sides, we get

Third side =
`(√(3) d)/(2)`

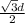
d is the hypotenuse. So

`(√(3) )/(2) = (Thirdside)/(Hypotenuse)`

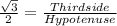
Here third side is the Adjacent side.

So, cos 30 =
`(√(3) )/(2)`