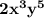Question

Which expression is the greatest common factor (GCF) of the terms of trinomial 12x^7y^9 + 6x^4y^7 - 10x^3y^5

Answer 1

The greatest common factor is 2. 2x^3y^5

Answer 2

Answer: 2.
`\mathbf{2x^3y^5}`

Explanation:

• Greatest common factor of any two or more expression is the largest common expression that divides them.

The given expression :
`12x^7y^9 + 6x^4y^7 - 10x^3y^5`

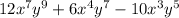
Term 1 :
`12x^7y^9`

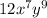
Term 2 :
`6x^4y^7`

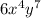
Term 3:
`- 10x^3y^5`

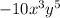
Lowest power of x = 3

Thus , The highest common power of x =
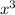`x^3` (i)

Lowest power of y = 5

The highest common power of y =
`y^5` (ii)

Greatest common factor of 12, 6 , -10= 2 [Because 2 is the largest number that divides all of them] (iii)

From (i) , (ii) , (iii) , we have

Greatest common expression :
`2x^3y^5`

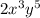
Hence, the correct answer is 2.
`\mathbf{2x^3y^5}`