Question

You and some friends are enjoying a trip to the water park on a hot summer day. Upon arrival, you decide you want to try the fasted and scariest water slide they have. To ride this water slide, a rider stands on a retractable floor and leans up against an upmost vertical portion of water slide, that makes an angle of approximately 84 degrees with the horizontal. The operator presses a button, the floor is retracted, the riders slide straight at the angle for approximately 6.3 meters until they are dropped into the twisting turning water slide. You (m = 62 kg) start at the top from rest. If the coefficient of kinetic friction between you and the slide is 0.12, how fast are you moving at the end of the straight portion of the slide?

Answer 1

First, draw a force diagram to identify the forces acting on the rider.

There are three forces acting on the rider: the rider's weight, the normal force and the friction force.

Using the surface of the slide as the horizontal axis, apply Newton's Second Law of Motion to find the acceleration of the rider.

The forces on the vertical axis (in the direction of the normal force) must balance out.

The vertical component of the weight is mg*cos(84º) and the horizontal component of the weight is mg*sin(84º). Then:

`\begin{gathered} \Sigma F_y=F_N-mg\cos\theta \\ \\ \Sigma F_y=0 \\ \\ \Rightarrow F_N=mg\cos\theta=(62kg)(9.8(m)/(s^2))\cos(84º)=63.5N \end{gathered}`

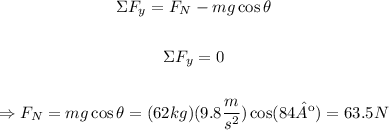
For the horizontal axis, the forces acting on the rider are the friction and the horizontal component of the weight:

`\begin{gathered} \Sigma F_x=mg\sin\theta-f \\ \\ \Sigma F_x=ma \\ \\ \Rightarrow ma=mg\sin\theta-f \end{gathered}`

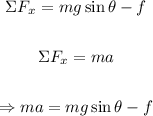
On the other hand, the friction is given by the product of the normal force and the coefficient of kinetic friction:

`f=\mu F_N=\mu mg\cos\theta`

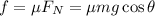
Then:

`\begin{gathered} ma=mg\sin\theta-\mu mg\cos\theta \\ \\ \Rightarrow a=g(\sin\theta-\mu\cos\theta) \end{gathered}`

Replace g=9.8m/s^2, μ=0.12 and 84º for the angle to find the acceleration of the rider:

`a=(9.8(m)/(s^2))(\sin(84º)-0.12\cos(84º))=9.62(m)/(s^2)`

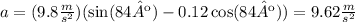
An object under constant acceleration that travels a distance d starting at rest will have a final speed given by:

`v_f=√(2ad)`

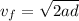
Replace a=9.62m/s^2 and d=6.3m to find the speed at the final portion of the slide:

`v_f=\sqrt{2(9.62(m)/(s^2))(6.3m)}=11(m)/(s)`

Therefore, your speed at the end of the straight portion of the slide would be equal to 11m/s.