Question

A quadratic equation is shown below:

4x^2 − 12x + 10 = 0

Part A: Describe the solution(s) to the equation by just determining the radicand. Show your work. (5 points)

Part B: Solve 2x^2 − 13x + 21 = 0 by using an appropriate method. Show the steps of your work, and explain why you chose the method used. (5 points)

Answer 1

A.
the radicand is b²-4ac
if it is in form ax²+bx+c

when it is
greater than 0, then 2 real roots
equal to 0, then 1 real root
less than 0, then no real roots

so
a=4
b=-12
c=10

b²-4ac=(-12)²-4(4)(10)=144-160<0
so 0 real roots



B.
using quadratic formula because it is easier
for
ax²+bx+c=0

`x=(-b+/-√(b^2-4ac))/(2a)`

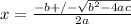
so

for 2x²-13x+21
a=2
b=-13
c=21


`x=(-(-13)+/-√((-13)^2-4(2)(21)))/(2(2))`

`x=(13+/-√(169-168))/(4)`

`x=(13+/-√(1))/(4)`

`x=(13+/-1)/(4)`
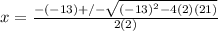
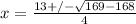
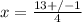
x=(13+1)/4 or (13-1)/4
x=14/4 or 12/4
x=7/2 or 3