Question

The question says "Throughout Lewis Carroll's book, Alice's Adventures in Wonderland, Alice's size changes. Her normal height is about 50 inches tall. She comes across a door, about 15 inches high, that leads to a garden. After drinking a potion, Alice's height changes to 10 inches so she can visit the garden. How tall would the door have been in Alice's normal world? Justify your answer and provide mathematical evidence." I don't comprehend what i'm supposed to do here

Answer 1

Using the idea of similarity, we can determine the height of the door in the normal world.

Given:

Normal height of Alice= 50 inches

Height of the door outside the normal world = 15 inches

Height of Alice after drinking the portion = 10 inches

Let the height of the door in normal world be x

`\begin{gathered} Normal\text{ height of Alice }\propto\text{ Normal height of the door} \\ \text{Height of Alice after drinking the portion }\propto\text{ Height of the door outside the normal world} \end{gathered}`

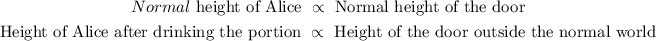
The constant of proportionality should be equal. Hence, we can write:

`(50)/(x)\text{ = }(10)/(15)`

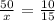
Ssolving for x:

`\begin{gathered} 10x\text{ = 750} \\ x\text{ = 75 inches} \end{gathered}`

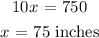
Answer: 75 inches