Answer:
In 14 minutes ride almost last.
Explanation:
The angle of elevation from the bottom of a scenic gondola ride to the top of a mountain is 22°
f the vertical distance from the bottom to the top of the mountain is 689 feet and the gondola moves at a speed of 130 feet per minute.
Please see the attachment for the figure.
Using trigonometry identity

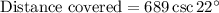
Speed=130 ft/min
We need to find time to ride last.


Thus, In 14 minutes ride almost last.