Question

A photographer points a camera at a window in a nearby building forming an angle of 42° with the camera platform. if the camera is 52 m from the building, how high above the platform is the window, to the nearest hundredth of a meter?

Answer 1

46.82 m

Explanation:

Given : A photographer points a camera at a window in a nearby building forming an angle of 42° with the camera platform.

To Find: if the camera is 52 m from the building, how high above the platform is the window, to the nearest hundredth of a meter?

Solution:

Refer the attached figure.

A photographer points a camera at a window in a nearby building forming an angle of 42° with the camera platform i.e. ∠ACB = 42°

The camera is 52 m from the building i.e. BC = 52 m

Now we are supposed to find how high above the platform is the window i.e. AB

In ΔABC

Using trigonometric ratio

`Tan \theta = (Perpendicular)/(base)`

`Tan 42^(\circ) = (AB)/(BC)`

`Tan 42^(\circ) = (AB)/(52)`

`0.9004 = (AB)/(52)`

`0.9004 * 52 =AB`

`46.8208 =AB`

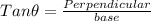
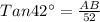
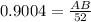
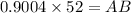
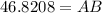
Thus the window is 46.82 m above the platform.

Answer 2

the base is 52 ft and the angle is 42

to find the height

multiply 52 by the tangent of 42

52 x tan(42) = 46.821,

round to nearest hundredth = 46.82 feet