Question

The height in feet of a baseball can be modeled by the function y = -16t^2 + 64t, where t is the time in seconds after the ball is hit. Find the baseball's maximum height and the time it takes to reach this height. Then find how long the baseball is in the air. a. 140 ft: 3 s: 65 b. 100 ft 1 s 2 s c. 64 ft: 2 s 4 s d. 164 ft 4 $ 8 8

Answer 1

`y=-16t^2+64t`

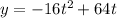
Factor the equation:

`y=-16t(t-4)`

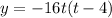
Equal to 0 as the height y is 0 in the moment the baseball is hit and in the moment the ball falls again:

`\begin{gathered} -16t(t-4)=0 \\ \\ \end{gathered}`

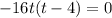
Fins the solutions for t:

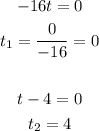
`\begin{gathered} -16t=0 \\ t_1=(0)/(-16)=0 \\ \\ t-4=0 \\ t_2=4 \end{gathered}`Then, you have how long the baseball is in the air: 4s

As the total time is 4: the time when the ball is in the maximun height is the half of this time (because the ball ups in the same time that falls.

Time of maximum hight: 2s

You use this time to find the maximum height:

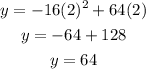
`\begin{gathered} y=-16(2)^2+64(2) \\ y=-64+128 \\ y=64 \end{gathered}`The maximum height is 64ftCorrect answer c.