Before we solve the system, let's verify if it has a solution, let's do the determinant test:
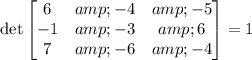
The determinant is 1, so it's different from zero, then the system has a unique solution.
Now let's determine the unique solution, I'll solve it using Cramer's Rule, because we already have the determinant of the coefficient matrix
Then
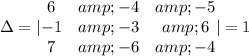
Now let's evaluate the determinants with the coefficients
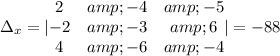
Now the variable y
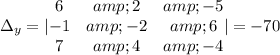
And the last one
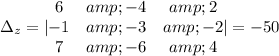
The solution will be
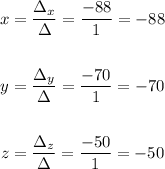
Final answer:
Only one solution
x = -88
y = -70
z = -50