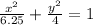The standard form of equation of an ellipse is in the form:
[(x – h)^2] / a^2 + [(y – k)^2] / b^2 = 1
Where, h and k are the center points, and a and b are one half the length of the major and minor axis.
Since height is 4 units and width is 5 units, therefore:
a = 5 / 2 = 2.5
b = 4 / 2 = 2
and h = k = 0 (at the origin)
The standard equation then becomes:
x^2 / (2.5)^2 + y^2 / 2^2 = 1
x^2 / 6.25 + y^2 / 4 =1