Question

A positive integer is 48 more than 23 times another. Their product is 12188. Find the two integers.

Answer 1

Given

A positive integer is 48 more than 23 times another.

Their product is 12188.

To find the two integers.

Step-by-step explanation:

Let x and y be the two positive integers.

Since a positive integer is 48 more than 23 times another.

Then,

`y=23x+48\text{ \_\_\_\_\_\lparen1\rparen}`

Also, since their product is 12188.

Then,

`\begin{gathered} xy=12188 \\ x(23x+48)=12188 \\ 23x^2+48x-12188=0 \\ 23x^2+554x-506x-12188=0 \\ x(23x+554)-22(23x+554)=0 \\ (23x+554)(x-22)=0 \\ x=22(\because x\text{ is a positive integer}) \end{gathered}`

That implies,

`\begin{gathered} y=23x+48 \\ y=23*22+48 \\ y=554 \end{gathered}`

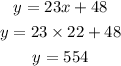
Hence, the two integers are 22 and 554 respectively.