Question

From the table below, determine whether the data shows an exponential function. Explain why or why not.

(x) -5, -4, -3, -2
(y) 0.5, 2, 8, 32

A) Yes; the domain values are at regular intervals and the range values have a common factor 8.
B) Yes; the domain values are at regular intervals and the range values have a common factor 4.
C) No; the domain values are not at regular intervals.
D)
No; the domain values are at regular intervals and the range values have a common factor 4.

Please help, and please give me an explanation on the answer you choose because I need to make corrections. Please.

Answer 1

B) Notice how you can get the next value multiplying by 4 each time, while x changes by one:

0.5*5=2, 2*4=8, 8*4=32

This function is 4^(x+4)*2 = 512*4^x, 512*4^(-5)=512/1024=0.5, it works!

Answer 2

Option B- Yes; the domain values are at regular intervals and the range values have a common factor 4.

Explanation:

Given : The data

(x) -5, -4, -3, -2

(y) 0.5, 2, 8, 32

To find : The data shows an exponential function or not

Solution :

The general form of an exponential form is
`y=ab^x`

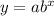
To check whether the data give the exponential function we form equation with the help of two points and verify the other two points .

`y=ab^x`

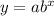
Let x= -5 and y=0.5

`0.5=ab^(-5)`

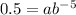
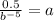`(0.5)/(b^(-5))=a` ......[1]

Let x= -4 and y=2

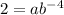
`2=ab^(-4)`

`(2)/(b^(-4))=a` .........[2]

Equate LHS because RHS is equal in equation [1] and [2]

`(2)/(b^(-4))=(0.5)/(b^(-5))`

`(b^(-4))/(b^(-5))=(2)/(0.5)`

`b=4`

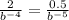
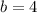
Put back in [2]

`(2)/(4^(-4))=a` .

`a=2*4^4`

`a=2*256=512`

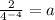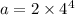
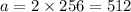
a=512 and b=4

Exponential function -
`y=4(512)^x`

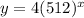
To verify this function put

1) x=-3

`y=512(4)^(-3)`

`y=\farc{512}{64}`

`y=8`

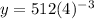
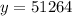
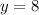
The point satisfied.

2) x=-2

`y=512(4)^(-2)`

`y=\farc{512}{16}`

`y=32`

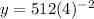
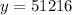
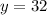
The point satisfied.

Therefore, The given data is an exponential function
`y=4(512)^x`

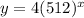
The domain values are at regular intervals and the range values have a common factor 4 because b=4 and the change happen but value of b remain same.

Hence, Option B is correct.

Yes; the domain values are at regular intervals and the range values have a common factor 4.