Question

Which equation below would produce thefollowing graph?A) f(2)=-(2+4)(3-1)(-5)B) f(z) = (2+4)(z-1)(-5)C) f(3) = (2-4)(2+1)(2+5)D) f(3) = -(2-4)(2+1)(2+5)

Answer 1

If we take the first option of the question, we have the following zeros or points passing through the x-axis:

`f(x)=-(x+4)\cdot(x-1)\cdot(x-5)=0`
`x+4=0,x-1=0,x-5=0`

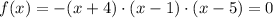
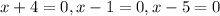
We then have:

`x=-4,x=1,x=5`

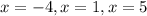
These points coincide with the ones in the graph.

The expansion of this equation is:

`f(x)=-x^3+2x^2+19x-20_{}`

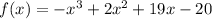
If we give some points to the equation at points x = -6, x = -3, x = 0, x = 3, x = 6, we have:

f(-6) = 154

f(-3) = -32

f(0) = -20

f(3) = 28

f(6) = -50

And all these values adjust to the proposed graph.

Therefore, the equation for option A would produce the proposed graph.

This is a way to solve this question. We can also make use of the derivatives of the first or of the second-order to find if this equation produces this graph.