Question

Really need help solving this Struggling It’s from my trig prep book

Answer 1

Start making the graph of the situation

from this, we can understand that x is Coreys' initial distance, z is Coreys' final distance, and y will be how many feet had Corey to step back in order to gain a better view.

Using the red triangle we find x through the tan of the given angle

`\begin{gathered} \tan \theta=(op)/(ad) \\ \tan 68=(80)/(x) \\ x=(80)/(\tan 68) \\ x\approx32.32 \end{gathered}`

Using the blue triangle we find z through the tan of the given angle the same way as before

`\begin{gathered} \tan \theta=(op)/(ad) \\ \tan 41=(80)/(z) \\ z=(80)/(\tan 41) \\ z\approx92.03 \end{gathered}`

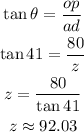
finally, find y as the difference between z and x

`\begin{gathered} z=x+y \\ y=z-x \\ y=92.03-32.32 \\ y=59.71 \end{gathered}`

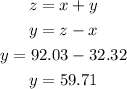
Corey had to go back 59.71 ft to gain a better view.