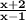Question

Simplify completely (7x²+11x-6)/(7x²-10x+3)

Answer 1

One way of simplifying the given expression is by factoring them, and then simplifying the common terms.

So, we need to write:

`\begin{gathered} 7x^(2)+11x-6=7(x-a)(x-b) \\ \text{and} \\ 7x^(2)-10x+3=7(x-c)(x-d) \end{gathered}`

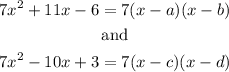
The constants a and b are the zeros of the first expression, and the constants c and d are the zeros of the second expression.

So, we can find those zeros using the quadratic formula. We obtain, for the first expression:

`\begin{gathered} x=\frac{-11\pm\sqrt[]{11^(2)-4(7)(-6)}}{2(7)} \\ \\ x=\frac{-11\pm\sqrt[]{289}}{14} \\ \\ x=(-11\pm17)/(14) \\ \\ a=(-11-17)/(14)=-2 \\ \\ b=(-11+17)/(14)=(6)/(14)=(3)/(7) \end{gathered}`

And, for the second expression, we obtain:

`\begin{gathered} x=\frac{-(-10)\pm\sqrt[]{(-10)^(2)-4(7)(3)}}{2(7)} \\ \\ x=\frac{10\pm\sqrt[]{16}}{14} \\ \\ x=(10\pm4)/(14) \\ \\ c=(10-4)/(14)=(6)/(14)=(3)/(7) \\ \\ d=(10+4)/(14)=1 \end{gathered}`

Then, we can write:

`\begin{gathered} 7x^2+11x-6=7(x-(-2))(x-(3)/(7))=7(x+2)(x-(3)/(7)) \\ \\ 7x^2-10x+3=7(x-(3)/(7))(x-1) \end{gathered}`

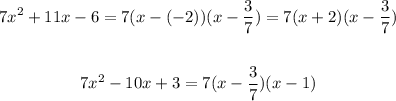
Thus, the given function can be simplified as follows:

`(7x²+11x-6)/(7x²-10x+3)=(7(x+2)(x-(3)/(7)))/(7(x-(3)/(7))(x-1))=(x+2)/(x-1)`

Therefore, the answer is:

`\mathbf{(x+2)/(x-1)}`