Question

Two concentric spheres have radii of 5" and 6". find the volume of the space between them. (4/3) cubic inches (91/3) cubic inches (364/3) cubic inches

Answer 1

Volume of a sphere = (4/3) pi r^3

required volume = (4/3) pi (6^3-5^3)

= (364/3) * pi cu ins.

Answer 2

Option (3) is correct.

The volume of the space between them is
`(364)/(3)\pi`

Explanation:

Given : Two concentric spheres have radii of 5" and 6".

We have to find the volume of the space between them.

We find the volume of both concentric spheres and subtract smaller volume from bigger volume.

We know Volume of sphere =
`(4)/(3)\pi r^3`

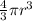
Thus, for sphere with radius 5 inches

Volume is given as

Volume of sphere =
`(4)/(3)\pi (5)^3`

Volume of sphere =
`(4)/(3)\pi\cdot 125`

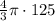
On simplifying, Volume of sphere =
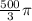`(500)/(3)\pi` cubic inches.

Thus, for sphere with radius 6 inches

Volume is given as

Volume of sphere =
`(4)/(3)\pi (6)^3`

Volume of sphere =
`(4)/(3)\pi\cdot 216`

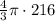
On simplifying, Volume of sphere =
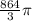`(864)/(3)\pi` cubic inches.

Thus, the volume of the space between them is Volume of sphere with radius 6 - volume of sphere with radius 5

Thus, the volume of the space between them =
`(864)/(3)\pi-(500)/(3)\pi=(364)/(3)\pi`

Thus, option (3) is correct.