The expression for the volume of the box is:
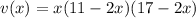
Mathematically, there is no restriction for the values of x, but phisically we know that x is a length and has a positive value, so x>0.
Also, we know that x can not be largest than half of the width, that is the smallest dimension of the piece of paper.
As the width is 11, we then know that x is smaller than 11/2=5.5.
In conclusion, the domain for x is:
![0To calculate the maximum volume for the box we have to derive the volume function and equal to zero:[tex]\begin{gathered} v(x)=x(11-2x)(17-2x) \\ v(x)=x(11\cdot17-11\cdot2x-2x\cdot17+4x^2) \\ v(x)=x(4x^2-56x+187) \\ v(x)=4x^3-56x^2+187x \end{gathered}]()
![\begin{gathered} (dv)/(dx)=4(3x^2)-56(2x)+187(1)=0 \\ 12x^2-112x+187=0 \\ x=\frac{-(-112)\pm\sqrt[]{(-112)^2-4\cdot12\cdot187}}{2\cdot12} \\ x=\frac{112\pm\sqrt[]{12544-8976}}{24} \\ x=\frac{112\pm\sqrt[]{3568}}{24} \\ x=(112)/(24)\pm(59.73)/(24) \\ x=4.67\pm2.49 \\ x_1=4.67-2.49=2.18\approx2 \\ x_2=4.67+2.49=7.16\approx7 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/t6mbry1o275kqlgirwe3.png)
The solutions are x=2 and x=7 approximately.
Because of our domain definition, we know that x=7 is not a valid solution, so the value of x that maximizes the volume is x=2.
The volume for x=0 is 0. Then, it will increase its value until x=2, where it reaches the maximum volume. From x=2 to x=5.5, the volume decrease until reaching v=0 at x=6.5.
Answer:
Domain: 0
Value of x that maximizes the volume: x=2.
From x=0 to x=2 the volume of the box increases.