Question

find the area of a triangle bounded by the y axis, the line f (x)= 8- 1/4x, and the line perpendicular to f(x) that passes through the origin

Answer 1

The line g(x), perpendicular to f(x), has a slope that is the negative reciprocal of the slope of f(x).

Since the slope of f(x) is -1/4, then the slope of g(x) is 4. Also, since g(x) passes through the origin (0, 0), then its equation is:

g(x) = 4x

So, those two lines intercept each other when

f(x) = g(x)

(-1/4)x + 8 = 4x

8 = 4x + x/4

8 = (16x + x)4

4 * 8 = 17x

32 = 17x

x = 32/17

Now, notice that f(x) has a y-intercept equal to 8. So, it intercepts the y-axis at y = 8, as shown below:

Now, we can find the area A of this triangle multiplying the side measuring 8 by the altitude of the triangle relative to that side, which is 32/17, and then divide it by 2:

`A=\frac{\text{side}\cdot\text{altitude}}{2}=(8\cdot(32)/(17))/(2)=4\cdot(32)/(17)=(128)/(17)\cong7.53`

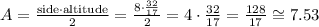
Therefore, the area is approximately 7.53.