Question

find the value of the ordinary annuity at the end of the indicated time period. the payment R, frequency of deposits m (which is the same as the frequency of compounding), annual interest rate r, and time period t are given. amount $600; quarterly; 7.6% six years. the value of the ordinary annuity is $_________ (round to the nearest cent as needed)

Answer 1

The formula of the value of the ordinary annuity is

`A=R\cdot((1+(r)/(m))^n-1)/((r)/(m))`

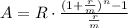
Where R represents the regular payments, m is the compounding periods, n is the number of regular payments, and A is the future amount. Let's use all the given values to find A. R = 600, r = 0.076 (7.6%), m = 4, and n = 24 (because we multiplied 6 years by 4).

`\begin{gathered} A=600\cdot((1+(0.076)/(4))^(24)-1)/((0.076)/(4)) \\ A=600\cdot((1+0.019)^(24)-1)/(0.019) \\ A\approx18,032.06 \end{gathered}`

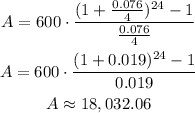
Therefore, the value of the ordinary annuity is $18,032.06.