Question

Determine the interval on which f(x) = ln(x) is integrable.

a. (0, ∞)
b. [0, ∞)
c. (−∞, 0) U (0, ∞)
d. All reals

Answer 1

a. (0, ∞)
....................................

Answer 2

Option: a is the correct answer.

a. (0, ∞)

Explanation:

We are given a logarithmic function f(x) as:

`f(x)=\ln x`

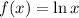
We know that the logarithmic function is defined for all the real values strictly greater than 0 i.e. x>0.

i.e. the function is defined for all positive real numbers.

i.e. the domain of the function f(x) is: (0,∞).

Also, we know that the function f(x) is integrable in it's domain and the integration is calculated by using the integration by parts.

i.e.

`\int\limits {\ln x} \, dx=\int\limits {1\cdot \ln x} \, dx\\  \\i.e.\\\\\int\limits {\ln x} \, dx=\ln x\cdot \int\limits {1} \, dx-\int\limits {(d)/(dx)\ln x} \cdot \int\limits {1} \, dx\\\\i.e.\\\\\int\limits {\ln x} \, dx=\ln x\cdot x-\int\limits {(1)/(x)\cdot x} \, dx\\\\i.e.\\\\\int\limits {\ln x} \, dx=x\cdot \ln x-\int\limits {1} \, dx\\\\i.e.\\\\\int\limits {\ln x} \, dx=x\cdot \ln x-x`

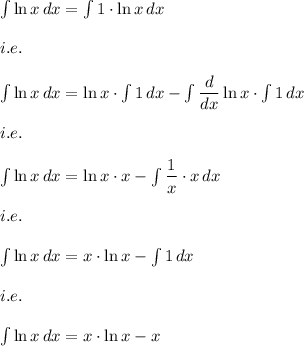
Hence, the answer is: Option: a