Question

Which equation describes the function represented by the table?

y = x - (-11)

y = 4x + 6

y = -7x - 5

y = -3x + 9

Answer 1

`\displaystyle y=-7x-5`

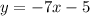
Explanation:

Equation of the Line

The equation of a line passing through points (x1,y1) and (x2,y2) can be found as follows:

`\displaystyle y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

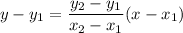
We'll take the first two points (-2,9) and (-1,2)

`\displaystyle y-9=(2-9)/(-1+2)(x+2)`

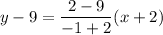
Operating:

`\displaystyle y-9=(-7)/(1)(x+2)`

`\displaystyle y-9=-7(x+2)`

`\displaystyle y-9=-7x-14`

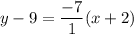
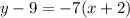
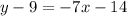
Adding 9:

`\boxed{\displaystyle y=-7x-5}`

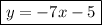
Substituting the last two points we can verify they also belong to the line.