Question

Which expression is equivalent to 1/144​

Answer 1

Answer: 1 12/12

Explanation:

Answer 2

`\displaystyle (12^5)/(12^7)`

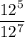
Explanation:

Equivalent Fractions

We need to recall the following properties of exponentials:

`\displaystyle (x^a)/(x^b)=x^(a-b)=(1)/(x^(b-a))`

Additionally, we have that 144=
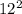`12^2`, thus the given expression

`\displaystyle (1)/(144)=(1)/(12^2)`

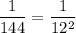
From the options presented, we have to find which one gives 12 squared in the denominator. It's apparent that the first choice:

`\displaystyle (12^5)/(12^7)=(1)/(12^(7-5))=(1)/(12^2)`

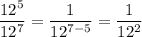
Is the correct choice.

Answer:

`\mathbf{\displaystyle (12^5)/(12^7)}`