Question

Consider the system of equations below.Y=x^2-2x+7Y=4x-10The graph of this stem confirms the solution from part a is imaginary.Explain why.

Answer 1

Not real but imaginary solutions because the equations do not intersect

Explanation:

We have the following system of equations:

`\begin{gathered} y=x^2-2x+7 \\ y=4x-10 \end{gathered}`

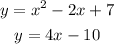
Graph each one through the graphing program and we have the following:

Both graphs do not intersect, therefore we can conclude that the answer in part a is correct, since the solution does not belong to the real numbers, but to the imaginary numbers.