Condition I
If f is defined at x=a, then,
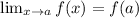
The above is true but it is not true for a stepwise function
Condition II
If f is continuous at x=a, then
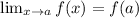
The second statement above is true for it meets the condition for continuity of a limiting function
Condition III
If f is differentiable at x=a, then
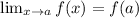
The third statement above is also true for a limiting function of differentiation.
Hence, statements II and III are true, OPTION D