Answer: d.
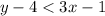 .
.
Explanation:
To find : The point (0,0) is a solution to which of the given inequalities.
Let's check all inequalities :
a.
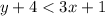
Substitute (x,y) = (0,0) , we get
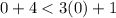
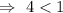 , which is wrong.
, which is wrong.
So , The point (0,0) is not a solution for
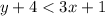 .
.
b.
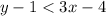
Substitute (x,y) = (0,0) , we get

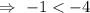
Multiply (-1) on both sides , we get
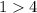 , which is wrong.
, which is wrong.
[Note : when we multiply a negative number to both sides of an inequality then the inequality sign gets reversed. ]
So , The point (0,0) is not a solution for
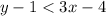 .
.
c.
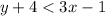
Substitute (x,y) = (0,0) , we get
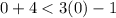
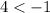 , which is wrong.
, which is wrong.
So , The point (0,0) is not a solution for
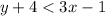 .
.
d.
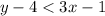
Substitute (x,y) = (0,0) , we get


Multiply (-1) on both sides , we get
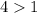 , which is correct.
, which is correct.
[Note : when we multiply a negative number to both sides of an inequality then the inequality sign gets reversed. ]
So , The point (0,0) is a solution for
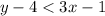 .
.