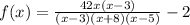Question

Write an equation of a rational function that satisfies these conditions (picture attached)

Answer 1

INFORMATION:

We have the next conditions

And we must find a rational function that satisfies all conditions

STEP BY STEP EXPLANATION:

1. Vertical and horizontal asymptotes:

To satisfies the first two conditions, we must put in the numerator and denominator of the function expressions which help us to satisfies these two conditions

`f(x)=(x)/((x+8)(x-5))`

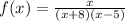
2. x-intercept and y-intercept:

To make that the function intercepts the x-axis in (-2, 0) and the y-axis in (0, -2) we must multiply the functions by 42 and subtract 2 from it

`f(x)=(42x)/((x+8)(x-5))-2`

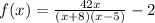
3. Hole:

To make the hole in the functions, we must multiply and divide by an expression which doesn't affect the function but makes a hole when x = 3

`f(x)=(42x(x-3))/((x-3)(x+8)(x-5))-2`

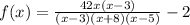
Finally, the graph would be

ANSWER:

`f(x)=(42x(x-3))/((x-3)(x+8)(x-5))-2`