Question

Find the point C along the segment from point A to point B that divides the segment into theratio 2 to 1

Answer 1

There are two ways to divide segment AB into two subsegments with a 2:1 ratio

`\begin{gathered} AC=2CB \\ \text{and} \\ 2AC=CB \end{gathered}`

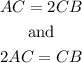
In general, the distance between two points on the plane is given by the formula below

`\begin{gathered} X=(x_1,y_1),Y=(x_2,y_2) \\ \Rightarrow d(X,Y)=\sqrt[]{(x_1-x_2)^2+(y_1-y_2)^2} \end{gathered}`

Furthermore, point C has to be on the same line as A and B, whose equation is

`\begin{gathered} y-3=(-3-3)/(6-(-3))(x-(-3)) \\ \Rightarrow y-3=-(2)/(3)(x+3) \\ \Rightarrow y=-(2)/(3)x+1 \end{gathered}`

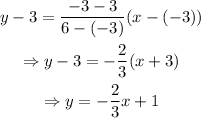
Additionally, the distance between A and B is

`d(A,B)=\sqrt[]{(-9)^2+(6)^2}=\sqrt[]{117}`

1) AC=2CB

`\begin{gathered} d(C,B)=\frac{\sqrt[]{117}}{3} \\ \Rightarrow\sqrt[]{(x-6)^2+(y+3)^2}=\frac{\sqrt[]{117}}{3} \\ \Rightarrow(x-6)^2+(y+3)^2=(117)/(9) \end{gathered}`

On the other hand, using the equation of the line,

`\begin{gathered} y=-(2)/(3)x+1 \\ \Rightarrow(x-6)^2+(-(2)/(3)x+4)^2=(117)/(3) \\ \Rightarrow(13)/(9)(x-6)^2=(117)/(3) \\ \Rightarrow(x-6)^2=27 \\ \Rightarrow x-6=\pm\sqrt[]{27} \\ \Rightarrow x=6\pm\sqrt[]{27} \end{gathered}`

However, x=6+sqrt(27)=11.19...-> out of the segment; therefore, the only valid value of x is

`x=6-\sqrt[]{27}`

Finding y,