ANSWER
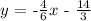
Step-by-step explanation
We have to find the equation of the line perpendicular to the given line:
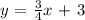
and passes through the point (-8, 6)
A line perpendicular to another line has a slope that is the negative inverse of the line.
The slope of the given line is 3/4, so the slope of the line we are looking for is -4/3
Now, we use the point slope method to find the equation:
y - y1 = m(x - x1)
where m = slope
(x1, y1) = point the line passes through
So, we have:
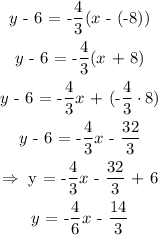
That is the equation of the line.