Question

What equation represents a line which is parallel to the line y =8/5x-1

Answer 1

Two parallel lines have the same slope.

`\begin{gathered} y=mx+b \\ m=\text{slope} \end{gathered}`

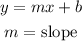
In the given equation the slope is:

`\begin{gathered} y=(8)/(5)x-1 \\ \\ m=(8)/(5) \end{gathered}`

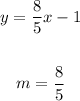
Then, you need to write the equations to slope-intercept form (solve for y) to identiy the slope:

Option 1

`\begin{gathered} 8x+5y=35 \\ 5y=-8x+35 \\ y=-(8)/(5)x+(35)/(5) \\ \\ y=-(8)/(5)x+7 \end{gathered}`

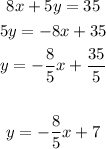
The slope in this one is -8/5. (Is not parallel to the given equation)

Option 2:

`\begin{gathered} 5x+8y=-24 \\ 8y=-5x-24 \\ y=-(5)/(8)x-(24)/(8) \\ \\ y=-(5)/(8)x-3 \end{gathered}`

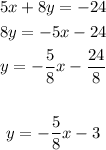
The slope in this one is -5/8. (Is not parallel to the given equation)

Option 3:

`\begin{gathered} 5x-8y=-32 \\ -8y=-5x-32 \\ y=(-5)/(-8)x-(32)/(-8) \\ \\ y=(5)/(8)x+4 \end{gathered}`

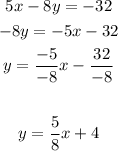
The slope in this one is 5/8. (Is not parallel to the given equation)

Option 4:

`\begin{gathered} 5y-8x=-35 \\ 5y=8x-35 \\ y=(8)/(5)x-(35)/(5) \\ \\ y=(8)/(5)x-7 \end{gathered}`

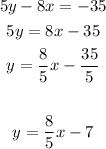
The slope in this one is 8/5. This line is parallel to the given equation.

Answer: Option 4 (5y-8x=-35)