Answer:
The cost of the computer in 3 years is $34.07
Explanation:
We have formula for depreciation.
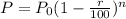
Where P is the final value, P_0 = initial value , r = rate of decrease and n = the number of years.
Given: P_0 = $50, r = 12 and n = 3
Now plug in the given values in the above formula, we get
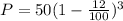
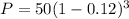
P =
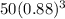
P = $34.07
Therefore, the cost of the computer in 3 years is $34.07